続・「6÷2(1+2)」をプログラマーが検証してみた

プログラミング

2023.05.032024.01.16

前回投稿から1年9カ月程度経っています。
最近6÷2aなどの2aについて、習ったときのことをふっと思い出したので改めて記事にしたいと思う。

はじめに

これは、投稿記事を読んでもらって考えてもらうのが目的であり、直球の例を示して「ふ～ん」となってしまうのを避けるためだ。
(前回の投稿記事のコメントに少し書いてしまってますが・・・)

また、6÷2aなどの2aについて、習ったときのことをふっと思い出したこともあり、今回は直球の例を示しつつ解説したい。

なお、前回の投稿記事を読まれた方でも新しい発見があるかもしれません。(2024/01/09変更)

「6÷2a」は次の分数になるのはご存じだと思う。

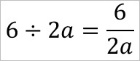
この「2a」が分母となることを学校(約40年前の小学校高学年? 中学校?)で習ったときの記憶を最近思い出した。

「6÷2a」の「2a」は単に「2×a」では無く、一つの数値のように扱わなければならない。

このため、「6÷2a」は「6÷2×a」ではないと言うことであり、分数で書いたとき「2a」は分母になるのだと。

直球で説明するために「6÷2a」から考えていく。

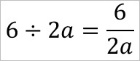
ここで、a=x+y だったとき、
6÷2a = 6÷2(x+y) となる。
6÷2x+y などとしてしまうと間違なのはご存じだと思う。

これを分数で書くと次になる。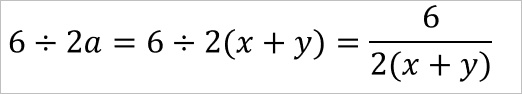

2aは分母になるので、それにa=x+yを適用するのも変わらない。

次にx=1だったとき、
6÷2(x+y) = 6÷2(1+y) となる

これを分数で書くと次なる。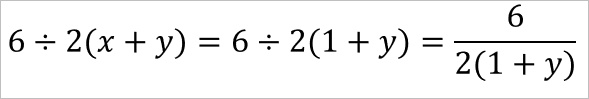

次にy=2だったとき、
6÷2(1+y) = 6÷2(1+2) となり、これが本題の式である。

上記の流れから分かるように、分数で書くと次になり、結果答えは1となる。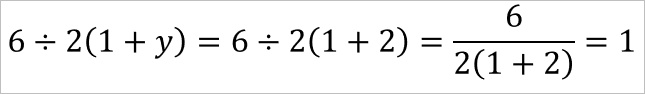

2a および 2(1+2)を1つの数値のように扱わなければならないのは変わらない。

これは、プログラミングでも大事で、「6÷2a」および変数に値を適用した「6÷2(1+2)」の答えが違ってしまうと、不良(=バグ)を作りこんでしまっていることになる。

「6÷2a」の「2a」は単に「2×a」では無く、一つの数値のように扱わなければならない

と私は教わったのだが、皆さんは、いかがだろうか?

もし、現役で教えている先生や、まだ教わってすぐの生徒さんが、この記事を読まれたのならば、下記のコメントにて、どう教えているか、どう教わったかをご連絡いただければ幸いです。
もちろん、先生や生徒さん以外の方のコメントも大歓迎です。

また、実は前回も今回もプログラミングの言語分野の「構文解析」を交えて解説しようとしていたのだけど、「焦点がブレる可能性がある」と考え、見送りました。

「構文解析」については将来的に投稿する予定なのでこちらに興味がある方はお待ち頂ければと思います。
※要望が多ければ記事作成の優先度が上がりますので、下記コメントにてお願いします。
まあ、わざわざ個人サイトを立ち上げてまで書きたいことが多すぎることもあり、「構文解析」について現在の優先度は低いです。

ご意見、ご要望、不具合などのご連絡は次からお願いします。

コメント
本投稿へ下部のコメントを書き込むからご連絡ください。
コメントは承認方式となっており、当方が承認しないと公開表示されません。
公開表示を希望されない方はその旨コメントに記述ください。
Twitter
ご連絡は @dratech2020 https://twitter.com/dratech2020 の該当ツイートに返信するか、ハッシュタグ「#プログラミングの深淵を求めて」を付けてツイートしてください。 (すぐに気が付かない場合がありますので、ご了承ください)