コラッツ予想の世界線を無限化する、iCollatz/Infinite Collatz/無限化コラッツ/アイコラッツとは?
目次
はじめに
発想は、「2進数なんて馴染みがないよ! 10進数で見やすくできないか?」からです。
「コラッツ予想のからくり」では、2進数で見ると直感的に解りやすいことを示しましたが、上記のような意見が出るであろうことは想定できます。
これを解決する手段として、iCollatzを提案します。
なお、スマホやPCなどのデジタル機器の根幹には2進数(2進法)が使われており、それらデジタル機器は2進数を用いている素振りを見せないように作られているだけです。
「馴染みがない」のではなく、「知らない」と言うのが正しいと言えます。
iCollatzの提案
本題に入る前に、コラッツ予想の世界線を無限化してしまったせいで、個人で確認できる範疇を遥かに超えています。
このため、執筆時点で未確認の基数(r: radix)と係数(k)と入力値(n)が無数にあります。
また、さすがに3進数や36進数にはなじみが無さ過ぎて確認作業の時間が足りません。
これらなどの関係から、公開当初の本式はVersion 0.5とさせていただきます。
iCollatz式

nは正の整数で、上下どちらかの式を適用した結果f(n)を次のnとして続けるのはオリジナルのコラッツ予想の式と同じです。
rは基数(Radix)で、2以上の正の整数を指定します。
「コラッツ予想のからくり」で示したのと同じように、r進数で見ると直感的に理解しやすくなります。
これは、r=10にすると10進数で見ると直感的に理解しやすいことを表しています。
nをrで割ったときの余りが0のときをMZR(Modulo ZeRo)と呼ぶこととし、0より大きい(余りは正の整数しかない)ときをMNZ(Modulo Non Zero)と呼ぶこととします。
これは、rが2とは限らないので、もう偶数/奇数とは呼べないためです。
kは、rより大きくないと見た目で増加傾向とならないため、k>rの条件が付いています。
また、k<r2の条件については、今後の投稿記事で明らかにします。
「2進数なんて馴染みがないよ! 10進数で見やすくできないか?」が発想の元なので、r=10,k=11の数列については本記事の末に記載します。
r=2,k=3のとき
r=2,k=3のとき、つまりコラッツ予想の世界線のときは、次の図のようになる。

このことから、iCollatz式の1つの世界線(r=2,k=3)が、コラッツ予想の式であることが分かる。
iCollatz[矯正:Correct]式
コラッツ予想[KAI]の提案 で示した式に相当するiCollatz式[矯正:Correct]は次のようになる。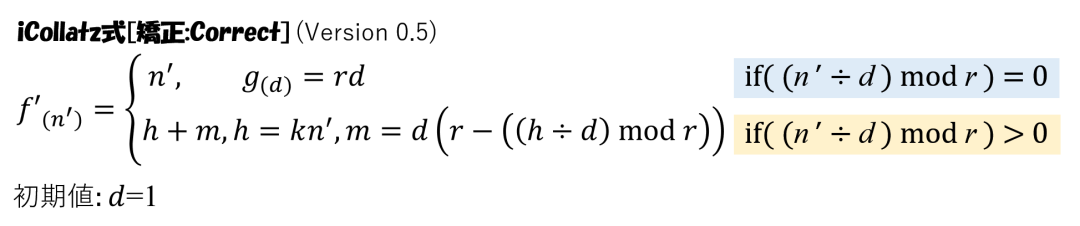
詳細は省略しますが、r進数で見た時、開始時のn’の1の位の桁の位置が変わらないように矯正するものです。
また、n’に注視すると、MZRの式は f'(n’)=n’ なので値はかわらず、MNZの式の f'(n’)=h+m を無限ループしているだけになる。(2023/07/01追記)
どうやってiCollatzの式はできたのか?
「2進数なんて馴染みがないよ! 10進数で見やすくできないか?」の発想を元にコラッツ予想の数列を分析します。
コラッツ予想の式のおさらい
コラッツ予想の式は、次である。
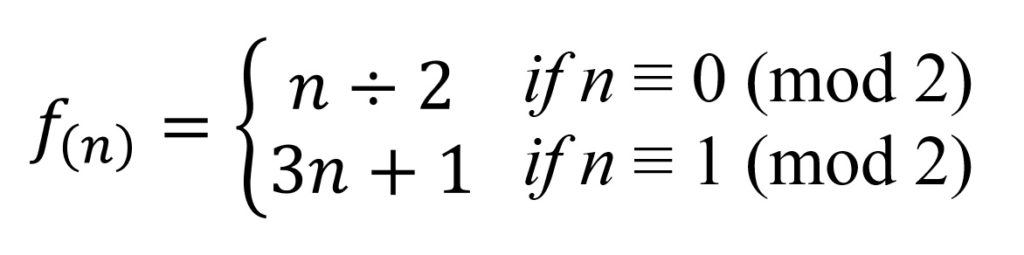
n=27のときの数列が次となる。
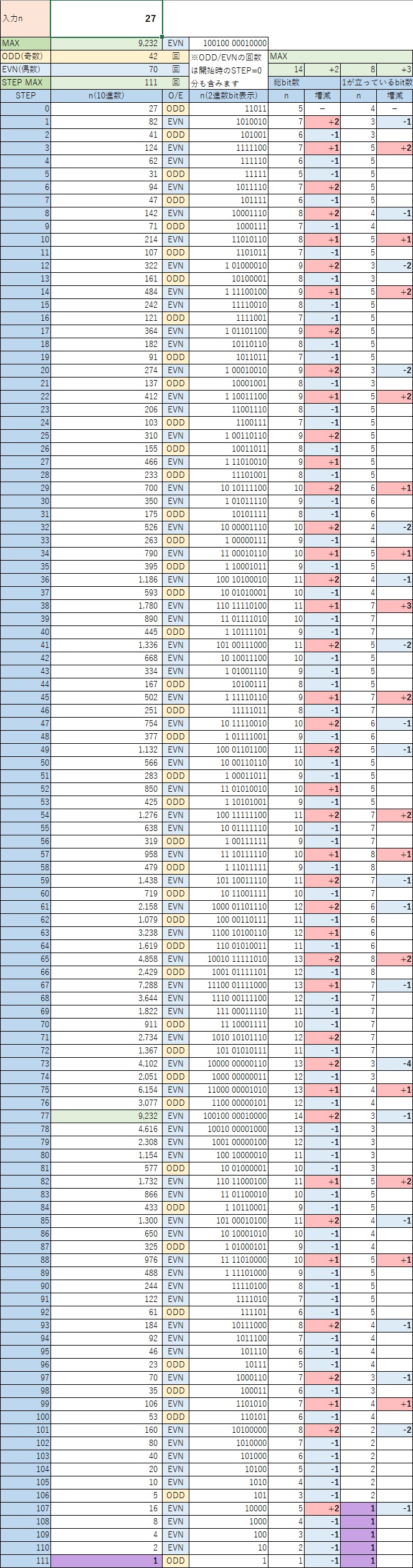
「2進数なんて馴染みがないよ! 10進数で見やすくできないか?」の発想を元にコラッツ予想の数列を分析する。
偶数側の式’n/2’
偶数側の式’n/2’は、こちら で示しているように2進数で見ると必ず右に1桁移動=右に1ビットシフトである。
右に1ビットシフトは、1度に一回しか発生しないので、最下位の桁=最下位ビットが’0’である限り、偶数側の式’n/2’が連続で適用される。
ここで、’n/2’の2と2進数の2が対応していることに気が付く。
奇数側の式’3n+1’
奇数側の式’3n+1’は、 こちら で示しているように’3n’は必ず奇数になり、’+1’すると結果f(n)は必ず偶数となる。
これを2進数で見ると、’3n’の最下位ビットは必ず’1’となり、それに’+1’すると必ず、桁上がりする(掛け算では無いので左に1ビットシフトではない)。
’+1’による桁上がりは、連鎖することがあるが、奇数側の式’3n+1’そのもの適用は連続することは無い。
r進数化
以上から、コラッツ予想の式から得られる数列は、2進数で見た時、偶数側の式’n/2’は右に1桁移動、奇数側の式’3n+1’は桁上がり、となっている。
これをr進数として置き換えていく。
偶数側の式’n/2’は、’n/r’となる。
奇数側の式’3n+1’の’3n’の’3’は係数kとし、’3n’→’kn’とする。
’+1’の部分に対して、’kn’をrで割った余りを求め、それをrから引いたものをknに足すことで桁上がりが発生する。
このように、変数を用いて説明すると分かり辛いとおもうので、r=10,k=11のときの例を示す。
’r=10’の時点で、’n’を’r=10’で割ったあまりは、0とそれ以外の1~9になるので、割り切れた0の方をMZR(Modulo ZeRo)とし、割り切れなかった余りが1~9のときはMNZ(Modulo Non Zero)とする。
MZR側の式は、’n/10’となる。
MNZ側の式は、’h=kn’が、’h=11n’となる。
例えば、’n=3’のとき、’h=kn=11*3=33’となる。
この値を下1桁に何かを足して桁上がりするようにすればよい。
このため、’h mod r=kn mod r=33 mod 10=3’なので、これを’r=10’から引くと、’m=r–(h mod r)=10-3=7’となる。
’33’と’7’を足すと’40’となり、桁上がりし、’r=10’で割ったときの余りが’0’となるので、MNZ側の式が連続して適用されることはない。
これをまとめたのが、iCollatzの式となる。

r=10,k=11に対して、n=1~100で求めた数列を本記事の末に記載します。
最後に
iCollatzの発想そのものは「コラッツ予想のからくり」を執筆中には既にあり、桁上がり/右に1桁移動の動作となっていることをあえてまとめてきていない。
また、前回の「コラッツ予想の演算ツール」のソースコードの最初の部分が次のようになっている。
const CC_RADIX=2n;
const CC_ODD=3n;※’2n’や’3n’の’n’は、BigInt型の数値を表す接尾辞です。
奇数側の3は、CC_ODDなのに、偶数側の2は、CC_EVENまたは文字数を合わせるためのCC_EVNではなく、CC_RADIX(基数)となっていることに気が付かれた方はいるだろうか?
これらは、本件およびツール(近日予定)を公開することを前提にしていたものです。
前回の公開から間が空いてしまっている主な理由は次です。
- 80年以上証明されていないコラッツ予想に対して、その世界線(r=2,k=3)を無限化してしまって良いのだろうかとの悩み
- 少しやっては放置、を繰り返していた。
- 私と同様の考え(閃き)に至る人物が現れるか?の好奇心
iCollatzとは関係の無い都合により、こちらに割く時間が取れなくなりそうなこと、前回公開から時間が経ってしまっているので、iCollatzは公開してしまおうとの流れです。
このため、本格的に作業したのは、ここ1、2カ月(2023/05~06)ぐらいです。
なお、本件は数学の発展に寄与できればと思い、オープン(透明性のある)かつ無料で公開します。
ただし、著作権を放棄したわけではありません。
記事参照/ツール利用は無料ですが、自由にして良いわけではありません。(It’s open and free, but it’s not freedom.)
なお、知的財産権的に、単なる数式のみは特許権も著作権も主張できません。
このため、数式のみは自由にすることが可能です。
ただし、その説明文などは著作権が主張できますので自由にすることはできません。
ご意見、ご要望、不具合などのご連絡
ご意見、ご要望、不具合などのご連絡は次からお願いします。
- コメント
本投稿へ下部の コメントを書き込む からご連絡ください。
コメントは承認方式となっており、当方が承認しないと公開表示されません。
公開表示を希望されない方はその旨コメントに記述ください。 - Twitter
ご連絡は @dratech2020 https://twitter.com/dratech2020 の該当ツイートに返信するか、ハッシュタグ「#プログラミングの深淵を求めて」を付けてツイートしてください。 (すぐに気が付かない場合がありますので、ご了承ください)
関連投稿
r=10,k=11の数列
(2023/06/27 表の表示方法を変更し関連する文章を変更しました)
まだまだ検証不足であるが、r=10,k=11のときのn=1~100までの数列を次に示す。
n=1のときの数列が、「1を含むループ」である。
nの多くは、1に到達し、「1を含むループ」になるが、例外もある。
n=34,38,42,47,52,58などで開始したときは1を含まないループになる。
各数列をよく見ると、ループ内の最小値は42であることが分かるため、「42を含むループ」と呼ぶこととする。
「42を含むループ」は、n=42の部分を見れば分かるが、96STEPで1つのループとなる。
「1を含むループ」を含まないループが発生することに対しての調査不足も含めiCollatzの式は、「r進数化」での説明のみを元にしたものなのでVersion0.5にしている理由の1つです。
ちなみに、n=9999999で開始すると、この「42を含むループ」になることが分かっている。
また、n=9…9(9を100桁)で開始すると、2860STEPで1に到達し「1を含むループ」になることが分かっている。
注:表が表示されるまでに時間がかかる場合があります。






コメント