コラッツ予想の証明に取り組むことにしたきっかけを主体にまとめてみました。
本サイトでは、PDF版とHTML版を公開します。
※「コラッツ予想」は「コラッツの問題」「3n+1問題」「3x+1問題」などとも呼ばれますが「コラッツ予想」に統一します。
PDF版
コラッツ予想の式
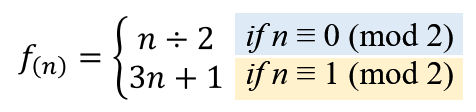
コラッツ予想とは、上記の式に対してすべての正の整数(※)のどれかのnで開始し結果を次のf(n)の入力として繰り返しても、最終的に1に到達する(正確には1→4→2→1→…の無限ループになる)と言う予想です。
“2”より”3″が大きいのに、増加し続けずに減少して”1″に到達してしまう。
このように矛盾した結果にたどり着くのは、何故なのでしょうか?
※:「自然数」と言うと’0’を含む場合と含まない場合があるため「正の整数(0を含まない)」に統一します。
第一印象
私のコラッツ予想の式に対する第一印象は「2進数との相性がよさそうだな」と同時に「3n+1の式の結果は増大するが2のべき乗(※)に収束するだけだよね?」だった。
※「累乗」とも言いますが「べき乗」に統一します。
この第一印象は次から来ている
- 偶数時の式n/2は2進数で見ると右に1ビットシフト(右に1桁移動)である。
- n=1に到達した後、1→4→2→1→…の無限ループになるが、出てくる数値はすべて2のべき乗である。
- 「すべての正の整数で開始してもn=1に到達する」のが正しい仮定すると、奇数時の式3n+1の結果が2のべき乗に収束するだけであろうことが想像できる。
コラッツ予想の式を見て、時間的に10秒ぐらいで(まるで呼吸をするかの如く)これを閃いた。
「なぜこんな簡単なことがわからないのだろうか?」と、「コラッツ予想が80年以上も証明されてない」ことの方が信じられなかった。
そう、私の論が正しければ、コラッツ予想の証明そのものは瞬殺だったと言っても過言ではない。
問題は、この論をどうやって説明したら伝わるかのみ苦労しているに過ぎない。
<補足>
- 右に1ビットシフトの例
偶数の数値を2進数で見ると最下位(一番右)の桁は必ず’0’である。
n/2はその最下位の’0’を削っていくが、’1’を含む文字列(ビットパターン)に変化は無い。
これは、確かに桁数は変わっているが数値の要素そのものに変化は無いと言うことです。
ちなみにプログラミングでは、下位の桁の’0’を削って、限られた演算精度にデータを収めることを簡略化とかモデル化と言い、結果を出力するときに通常は削ったものを元に戻すのですがコラッツ予想の式にはその仕組みがないため不思議に見える原因の1つとなっている。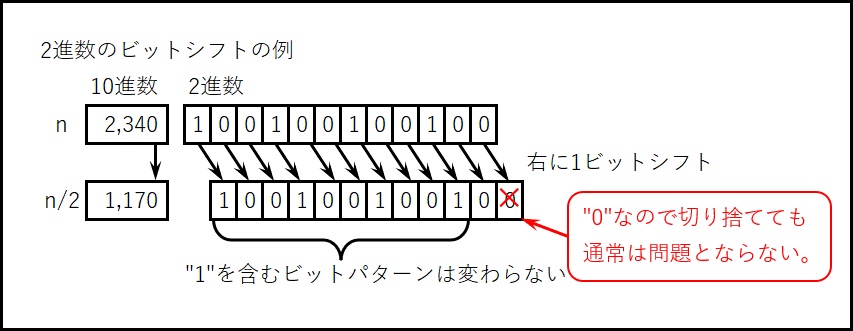
- 2のべき乗を2進数で見ると最上位(一番左)の桁が’1’で下位の桁には’0’が並ぶ。
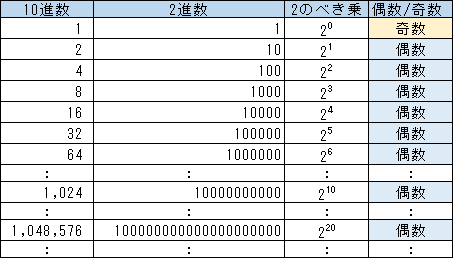
このように2のべき乗、つまり1,2,4,8,16,32,64… は数値が大きくなるほど10進数で見ると直感的に気が付きにくくコラッツ予想の数列が不思議に見える原因の1つとなっているが、2進数で見ると直感的に理解しやすい。
奇数時の式3n+1の結果が2のべき乗に収束する(最上位の桁のみに’1’)と偶数時の式n/2の右に1ビットシフト(最下位の桁の’0’を削る)の組み合わせで、結果としてn=1に到達する(その後1→4→2→1→…の無限ループになる)。
ちなみに、toString(2)などのメソッド(関数)で2進数の文字列を取得できるプログラミング言語が多いです。
「n=1になる」と言う表現について
私がコラッツ予想に関して文章を書くときに気を付けているのが「n=1になる」と言う表現を使わないことです。
「n=1に到達した後、1→4→2→1→…のループになる」のが正しいのであってn=1は到達点の一つでしかありません。
前者のような「n=1になる」という曖昧またはミスリードを誘う表現をすると目的(ゴール)を見失う可能性が高くなります。
プログラミングの上流工程で、最初にやることの1つが「要件定義」です。
要件は、自然言語(日本語など)で書くため、曖昧な表現やミスリードを誘う表現は回避し、より正確な表現にしなければならず、これが言い回しを注意する理由です。
第一印象の検証について
「3n+1の式の結果は増大するが2のべき乗に収束するだけだよね?」を証明の結果と仮定して、検証したものついては下記投稿記事および関連記事を参照ください。
コラッツ予想のからくりのまとめ(https://www.seekabypro.com/2021/12/18/collatz_mechanism_summary/)
iCollatz(無限化コラッツ)の提案 まとめ(https://www.seekabypro.com/2023/06/21/icollatz_summary/)
また、公開しているツールは簡易確認用のExcel版と本格確認用のWebブラウザ(BigInt)版がそれぞれあります。
後者のWebブラウザ(BigInt)版は、スパコンなどを使うことなく普段ご利用のブラウザで、開始時のnに10進数100桁や1,000桁(無量大数より遥かに大きい、垓(がい)つまり10進数20桁程度など可愛いもの)などの非常に大きい値を演算することが可能です(ブラウザの種類やマシン環境(メモリ量など)により制限がある場合があります)。
(注) 投稿記事/ツールは無料で参照/利用が可能です。
ただし、知的財産権(著作権)を放棄したわけではありませんのでご注意ください。
簡単に検証結果をまとめると、3n+1の「’3n’の増大が比較的小さく、2進数で見みたときに’+1’による桁上がり、および桁上がりの連鎖が発生し2のべき乗に収束する」ことを確認しており、仮定が正しい、つまりコラッツ予想の証明ができたと考えています。
なお、「3nの増大が比較的小さく」は、何と比べて小さいのか?
これを明確にし、コラッツ予想を完全証明するのがiCollatz(無限化コラッツ)を提案している理由です。
本文章の知的財産権(著作権)について
本文章は著作権で保護されています。
ただし、改変しない限り著作権法(第32条)に基づいた引用に該当するとみなし、再配布が可能です。
改変をした場合は、著作権法(第20条)違反になり、処罰される対象となる場合がありますのでご注意ください。
©2021-2023 プログラミングの深淵を求めて https://www.seekabypro.com/
©2021-2023 どらテク https://twitter.com/dratech2020
ご意見、ご要望、不具合などのご連絡
ご意見、ご要望、不具合などのご連絡は次からお願いします。
- コメント
本投稿へ下部の コメントを書き込む からご連絡ください。
コメントは承認方式となっており、当方が承認しないと公開表示されません。
公開表示を希望されない方はその旨コメントに記述ください。 - Twitter(現:X)
ご連絡は @dratech2020 https://twitter.com/dratech2020 の該当ツイート(ポスト)に返信するか、ハッシュタグ「#プログラミングの深淵を求めて」を付けてツイート(ポスト)してください。 (すぐに気が付かない場合がありますので、ご了承ください)






コメント