「6÷2(1+2)の解答は1なのか9なのか?」問題のまとめ

6÷2(1+2)=1にしかならないよ!!!
ところで6÷2a の分数表記で「2aが分母になる」のはなぜなのか覚えていますか?　
#何事も基本が大事 #30年遅いんだよ #Google検索バグってる
解決のヒントは、「何事も基本が大事」です。

本サイトでは、関連記事とPDF版とHTML版を公開します。(画像版はSNSのみ)

関連記事

本投稿は、この2つをまとめ、一部加筆したものです。

PDF版

基本を思い出してもらう

6÷2a を分数で書くと「2aが分母になる」のはご存じだと思います。
これは、「2aなどの表記は、1つの数値のように扱わなければならない」と言う基本があるからです。
それでは、本題の式「6÷2(1+2)」 を分数で書くとどうなるのでしょうか?

まずは、基本を思い出してもらうため「6÷2a」から解説します。

「6÷2a」と「6÷2×a」は違う式

(1) 6÷2a
(2) 6÷2×a
の2つの式が違うのはご存じですよね?

この違いを明確にするため、各式を分数で書きます。

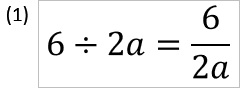
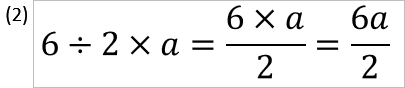
(1)は「2aが分母になる」が、
(2)は「2のみが分母になり、aは分子の6に掛け算することになる」
　　　これは÷と×の優先度が同じなので左から計算するためです。
　　　※約分すると6a/2=3aとなりますが分数のまま進めます。

分数で書くと、見た通り、この2つの式はまったく違い、2aは単に×を省略したものでは無いことが分かります。

では、(1)で「2aが分母になる」のは、なぜなのでしょうか?

その理由である基本を学校で「2aなどの表記は、1つの数値のように扱わなければならない」と教わりませんでしたか?
何事も基本が大事です。
このため、(1)は「2aが分母になる」のです。

以下、この基本を元に、本題の式「6÷2(1+2)」がどうなるのか順に１つずつ解説します。

a=3のとき

a=3のときに(1)と(2)の式はそれぞれどうなるでしょうか?

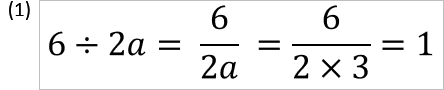
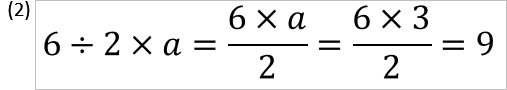
(1)の解答が1で、(2)の解答が9 (約分したとしても3a=3*3=9なので変わらない)となります。

(1)と(2)は式が違うので解答も異なります。

a=x+yのとき

次に、a=x+yのときはどうなるでしょうか?

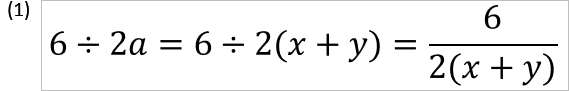
このように、aは「1a」でもあり1つの数値のように扱うのは変わりません、「2(x+y)」のように括弧を使って書くのが正しく、「2x+y」などのように括弧なしで書くと間違いなのはご存じだと思います。

x=1のとき

さらに、x=1のときはどうなるでしょうか?

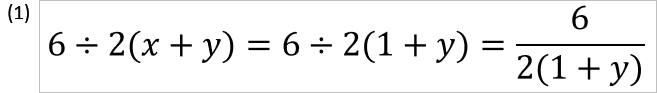
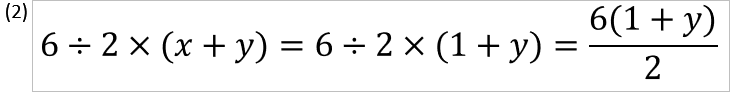
このように、x=1としても分数にする前と後で整合性は変わりません。

y=2のとき

さらに、y=2のときはどうなるのでしょうか?

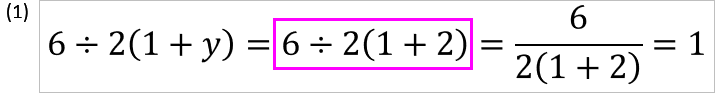
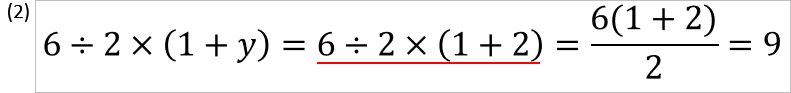
このように、(1)には本題の「6÷2(1+2)」の式がありますが、(2)にはありません。

(1)と(2)の式が違うことによって解答が異なる(1と9)のは当たり前です、変数の値が変わらないのに分数表記にしたら解答が異なってしまうのは数学ではありえないのはご存じだと思います。

解答が異なってしまうのは、(1)と(2)のように式が違うことに他ならないからです。

このように「6÷2(1+2)」の2(1+2)は元々2aで、2(1+2)も2aと同じく1つの数値のように扱う必要があり、2(1+2)=2×3=6となるため6÷2(1+2)=6÷6=1、つまり「6÷2(1+2)=1にしかならない」のです。

知識を知恵に昇華する

この(1)と(2)の違いは過去の実体験から気が付いたものです。

30年ぐらい前、C言語を実務で使い始めた頃に(1)のようにコーディングしなければならないところを間違って(2)のようにコーディングしてしまいました。

変数aに値(例3)を入れて、筆算で計算した(1)の解答(期待値=1)とテスト実行した(2)の解答(実行値=9)が違いました。

つまり、(1)と(2)の2つの式は違うため「コーディングが間違っている」のだと実感したことがあります。

「2aなどの表記は、1つの数値のように扱わなければならない」の基本があるため、(1)「6÷2a」の式をコーディングするときは「6/(2*a)」のように括弧を使って書かないと2aが1つの数値のように機能しないことに気が付きました。

基本を知識として知っていても、間違いを起こし、苦労する経験をしないと知恵(技術とも言う)として身に付かない実例として「知識を知恵に昇華する」を体験しました。

現在でも「6÷2(1+2)」の解答が1か9かで世界で論争になっているぐらいなので、当時の私の衝撃(※)は印象的な記憶として残っています。

(2024-01-18追記)
※:(1)は「2aが分母になる」ことを(知識として)知っていたのに、それを(知恵として)使いこなせてなかった衝撃です。
本「6÷2(1+2)の解答は1なのか9なのか?」問題自体は2011年ごろからあるのですが、使いこなせてないのは自分ぐらいだと思ってましたので、問題として論争になっていることに2021年まで気がつきませんでした。

　　　本問題に終止符を打つため、あえて挑発的に言わせてもらいます
　　　「30年遅いんだよ!!!」

Google検索バグってる

なお、「6÷2(1+2)=」((1)に該当)に対してGoogleの検索結果や計算機(電卓など)の結果で「6÷2×(1+2)=9」((2)に該当)のように間違いを返すものがありますが過去の私のように「コーディングが間違っている」からです。

おそらく、(1)と(2)の式が違うことを知らず、テスト/検証が足りないのだと思います。

要するに「バグってる」だけです。

(2024-01-19追記)
画像も貼っておきます。

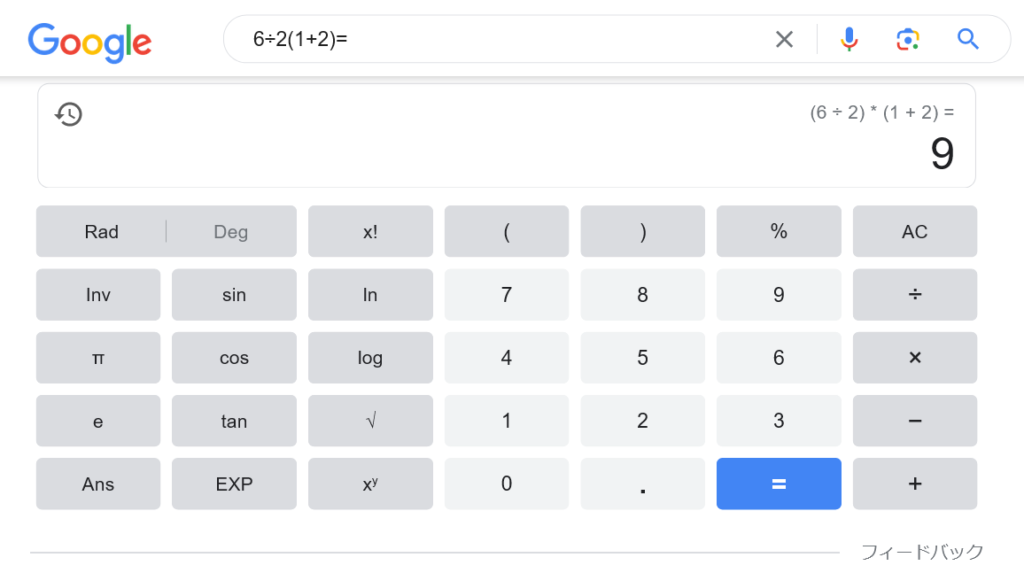
　　　あえて挑発的に言わせてもらいます
　　　「Google検索バグってる」(2024/01/15現在)

「6÷2(1+2)の解答は1なのか9なのか?」問題の個人的感想

「6÷2(1+2)の解答は1なのか9なのか?」問題そのものに対する私の個人的な感想は次です。

• そもそも基本を教わってないのか?
• それとも基本を忘れているのか?
• 本文のような論理展開ができないのか?
  つまり基本を知識としてしか知らず、知恵(技術)として身に付いていないのか?
  (基本を知恵として身に付けていれば2aと2(1+2)の違いなどの応用は簡単)
• 知識および知恵(技術)はあるが、他人がわからない(知らない/気が付いてない)ことに対してうまく説明ができないのか?　(私はココ、今回はうまく説明できているでしょうか?)

多くの方は、これらのいずれか、または複数が該当するのではないでしょうか?

まず、自分の立ち位置を認識し、基本を押さえつつ、状況に合わせて問題解決し改善するのが良いと思います。

本文章の知的財産権(著作権)について

本文章は著作権で保護されています。
ただし、改変しない限り著作権法(第32条)に基づいた引用に該当するとみなし、再配布が可能です。
改変をした場合は、著作権法(第20条)違反になり、処罰される対象となる場合がありますのでご注意ください。
©2021-2024 プログラミングの深淵を求めて https://www.seekabypro.com/
©2021-2024 どらテク https://twitter.com/dratech2020

ご意見、ご要望、不具合などのご連絡

ご意見、ご要望、不具合などのご連絡は次からお願いします。

• コメント
  本投稿下部の コメントを書き込む からご連絡ください。
  コメントは承認方式となっており、当方が承認しないと公開表示されません。
  公開表示を希望されない方はその旨コメントに記述ください。
  なお、スパムと認識したコメントは自動でブロックされますので用語にはご注意ください。
• Twitter(現:X)
  ご連絡は どらテク @dratech2020 https://twitter.com/dratech2020 の該当ツイート(ポスト)に返信するか、ハッシュタグ「#プログラミングの深淵を求めて」を付けてツイート(ポスト)してください。 (すぐに気が付かない場合がありますので、ご了承ください)