実際の例を用いながらそのからくりを解き明かす。
本記事に関連する新しい投稿があります(2023/07/05追記)
目次
特徴&論理
前回、 特徴と論理をまとめたので掲載しておく。
特徴
コラッツ予想の式から以下の特徴が抽出できる。
- [特徴1]偶数と奇数の2種類の数値を扱うこと
- [特徴2]n/2が2進数では”右に1ビットシフト”であること
- [特徴3]到達点の”1″、および、”1→4→2→1→…”の無限ループの各数値が、2のべき乗(1=20, 2=21, 4=22)であること
これらの特徴からコラッツ予想の式は”2進数”との親和性が高いことが分かる。
論理
コラッツ予想の式から以下の論理が導き出せる
- [論理A]nを2進数で見たとき、最下位ビット(20の桁)が”0″であれば偶数、”1″であれば奇数である
- [論理B]”n/2″は2進数では”右に1ビットシフト”であり、数値の要素となる”1″を含んだビットパターンは変わらない
- [論理C]”3n+1″の結果は必ず偶数となり、下位の桁のグループに2のべき乗を含む
- [論理D]”3n+1″の”+1″により、上位の桁のグループより下位の桁のグループの方が速く増加する
- [論理E:要証明]”3n+1″を無限に繰り返すと、nそのものが2のべき乗(“1″が立っているビットが1つ)に収束する
コラッツ数列の例
“33”の例
例として開始時の入力nに”33″を利用したコラッツ数列の場合で見ていく。
なお、nが”1″に到達した後も検証するので、”1→4→2→1→…”のループも数回繰り返したものを利用する。
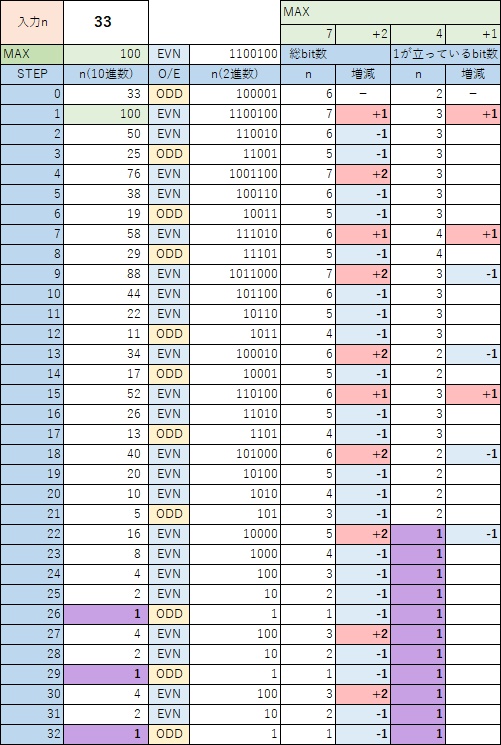
“33”の例に[論理A~E]を適用その1
上記の例に各[論理A~E]を適用したものが次となる。

以下、要点を抜粋して説明する。
- 開始時の入力n(STEP:0)の2進数の上位のグループを”1“、下位のグループを”1“とする
(注)上位のグループと下位のグループは直感的に理解しやすいようにしているものであり、グループ分けする法則などはない - STEP:0→1
[論理A]奇数のため”3n”と”+1″を実施し結果は次となる。
[論理C]下位のグループ”100“は偶数&2のべき乗である。
[論理D]上位のグループ”11“より下位のグループ”100“の方が”+1″の分速く増加する。 - STEP:1→2
[論理A]偶数
[論理B]右に1ビットシフトで下位の”0“を切り捨てる - 以降、[論理A]奇数と[論理A]偶数のうちどちらかを実施しつつ繰り返す
- STEP:6
n=”10011“の3nが”111001“となり下位のグループが上位のグループの侵食を開始する。 - STEP:12
n=”1011“の3nが”100001“となり下位のグループが上位のグループの侵食を完了する。 - STEP:22
[論理E:要証明]nそのものが2のべき乗(“1″が立っているビットが1つ)に収束していることを確認できる。
ただし、証明できるだけの情報が足りない。 - STEP:26
nが”1″に到達 - STEP:27以降
nが10進数では”4→2→1″、2進数では”100→10→1″と、2のべき乗(“1″が立っているビットが1つ)を保ったまま無限ループになる。
このままでは、まだ何か足りない。
コラッツ予想の深淵を求めようとしているのに、右に1ビットシフトで下位の”0“を切り捨ててしてしまっている。
コラッツ予想の全貌を見るためにはこの対策が必要となる。
“割り算の基本”と”右に1ビットシフト”の関係
“右に1ビットシフトで下位の”0“を切り捨て”の対策を検討するが、その前に確認して置くべきことがある。
前回の投稿で利用した10進数で”2,340/10″を計算するときの例で説明する。
”2,340/10″は、最下位の”0″を切り捨てし”234″を右に1桁移動したものである と説明した。
2,340 / 10 → 2340 の"0"を切り捨てでは、さらに”234/10″を実施したときはどうなるだろうか?
234 / 10 → 234 商が"23"で余りが"4"本来、割り算の答えは、”商と余り“が存在する。
余りの”4“については、どうするかその利用方法に応じて対策方法の検討が必要となる。
前者の”0“も余りが”0“なだけで、通常問題とならないため切り捨てているだけである。
では、”2,340/100″の場合はどうなるだろうか?
2,340 / 100 → 2340 商が"23"で余りが"40"このように余りは”40“である。
上記2つの例のように”1回では10で割ることしかできない“システムがあったとき、余りが”0“の時でもそれを記録してないとならない。
2回実施した結果、余りは”4“と”0“が揃ってないと”40“を導きだすことはできない。
この論理は2進数でも変わらない。
10進数で見たn/2は、2進数ではn/10であり、それは”右に1ビットシフト”であり、右にはみ出た分は、”余り”である。
例えば2進数でn=”1001 00100100″(10進数で”2,340″)としたとき、n/10(10進数で”2″)や n/1000(10進数で”8″)は次のようになる。
1001 00100100 / 10 → 1001 00100100 商が"1001 0010010"で余りが"0"
100 10010010 / 10 → 100 10010010 商が "100 1001001"で余りが"0"
10 01001001 / 10 → 10 01001001 商が "10 0100100"で余りが"1"
1001 00100100 / 1000 → 1001 00100100 商が "10 0100100"で余りが"100"
(注)コラッツ予想とは直接関係の無い割り算の例です。コラッツ予想の式は、”1回ではn/2することしかできない“システムである。
ただし、nが偶数(2で割った余りが”0“)のときのみしか、n/2、つまり”右に1ビットシフト”を実施できないので、余りは必ず”0“となる。
しかし、この”0“を記録することでコラッツ予想の全体像がより見えるのではないだろうか?
数値の基準点
もう1点確認して置くべことがある。
我々が数値を見るときの基準点はどこですか?
前回の投稿で、10進数の”1,048,576″を示しましたが、この数値を読むときは、どうしますか?
右側の最下位の桁=100の桁=1の桁(1の位)から左側の最上位の桁まで何桁あるか数えて、”百四万八千五百七十六”と読む。
数字の基準点は右側の最下位の桁であることはご存じの通りである。
これは2進数でも同じです。
右に1ビットシフト時の切り捨て分の”0″を記録
上記の “33”の例 では、コラッツ数列の全体を見たいのに捨ててしまっているものがあった。
“右に1ビットシフト”で切り捨てていたもの、つまりn/2の余りの”0″を記録すると今まで見えてなかったものが見えてくる。
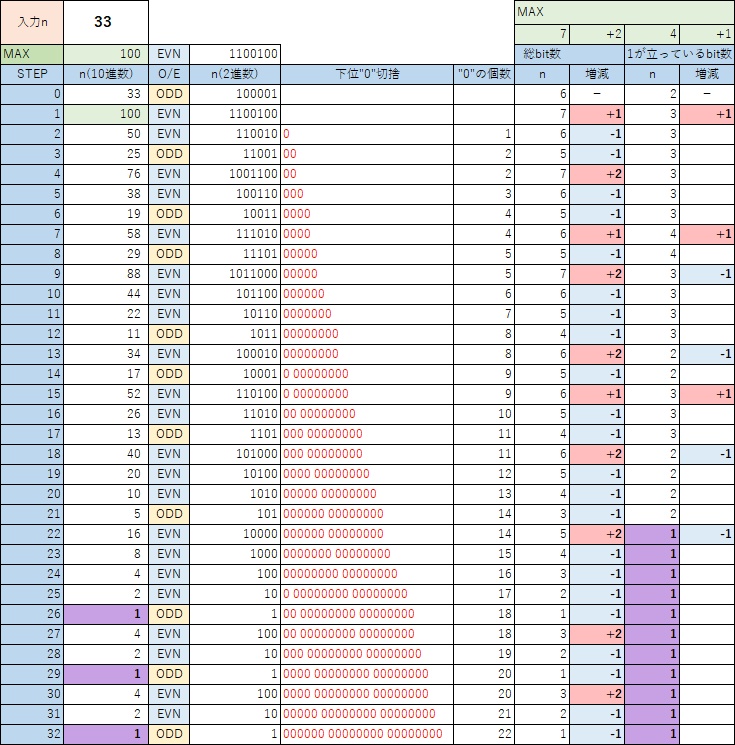
前述の”33″の例の表から、下位”0″切捨 と 切り捨て分の “0”の個数 の列を追加している。
STEP数が小さい間は良いが、STEPが大きくなにつれて”0″の個数が増えると見辛くなるので、切り捨て分の”0″の個数(nの側の”0″の個数は含まない)を並記している。
“33”の例に[論理A~E]を適用その2
上記の例に各[論理A~E]を適用したものが次となる。
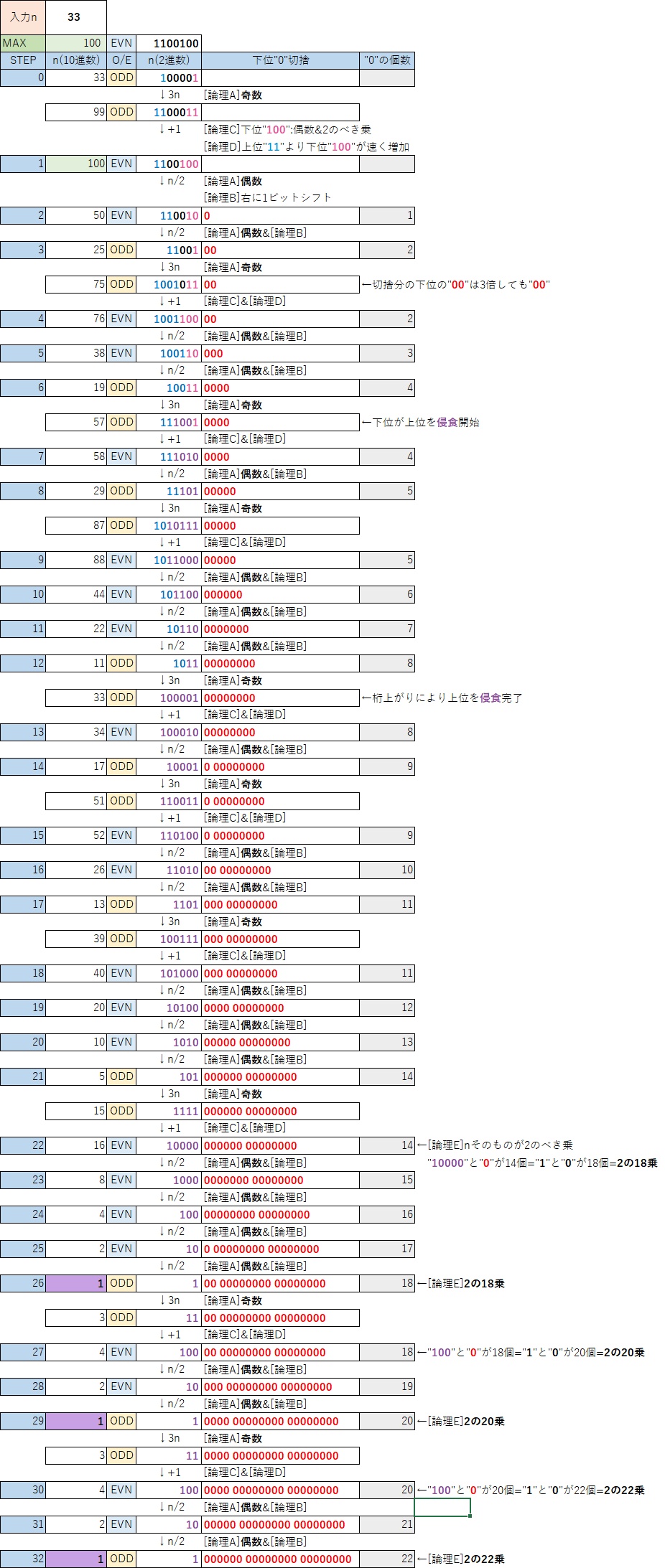
以下、”0“を記録して見えてきた部分を中心に抜粋して説明する。
- STEP:1→2
[論理A]偶数
[論理B]右に1ビットシフトで下位の”0“を切り捨てず、記録していく。
なお、”0“の個数はnが偶数となった回数と同じとなる。
表ではEVN(偶数)となったあとの処理のため1つ下の行にずらして表示している。
また、STEP:2時点のnは”右に1ビットシフト”しているため、数値の基準値がSTEP:0(開始時)の基準値より左に1ビットずれていることがわかる。 - STEP:3→4
[論理A]奇数のため”3n”を実施するが、切り捨て分の”00“を含めて3倍したとしてもその部分は”00“のままである。
また、ここまでにEVN(偶数)が2回発生していて、数値の基準値がSTEP:0(開始時)の基準値より左に2ビットずれている。
“+1″は数値の基準点(20の桁)に作用するため、この位置も同様に左に2ビットずれていることがわかる - STEP:22
[論理E]nそのものが”10000“となり、切り捨て分の”0“を含めて、218になっており、2のべき乗(“1″が立っているビットが1つ)に収束していることが確認できる。
この時点で[論理E]の証明は可能だが、基準点がずれているため理解が難しくなるので、証明は次回の投稿で説明する。 - STEP:26
nが”1″に到達するが、切り捨て分の”0″を含めるとSTEP:22から変わらず218のままである。
2のべき乗に対して”右に1ビットシフト”が複数回発生した結果、”1″に到達していることが確認できる。 - STEP:27
このSTEPからnが2のべき乗を保ったままの無限ループが開始する。
また、この時点で切り捨て分の”0“を含めると220になっていることが確認できる。 - STEP27以降
3回のSTEP毎に、nは10進数では”4→2→1″、2進数では”100→10→1″と見えるが、切り捨てられた”0“を含めると2のべき乗の指数部は2個ずつ増える。
2個ずつなのは、2進数で”100″の”0″の個数と対応している。
その他に次のことがわかる。
nが奇数時の”3n+1″の結果は[論理C]から必ず偶数となり、2のべき乗を下位のグループに含む。
その後、nが偶数時の”n/2″は[論理B]から”右に1ビットシフト”である。
このようにコラッツ数列では、奇数の次のSTEPは必ず偶数となるが、偶数は複数回続く場合がある。
“n/2″は単体で見ると”右に1ビットシフト”でしかないが、それが複数回発生すると、どうなるのだろうか?
“右に1ビットシフト”では数値の要素となる”1″を含んだビットパターンに変化は発生しないことを含めて、それが複数回発生すると“1”を含んだビットパターンの一番右にある”1″を数値の基準点となる20の桁まで移動(シフト)する機能と言える。
次にSTEP:9~12を抜粋したものを示す。

この部分は”1011″のビットパターンを基準点(20の桁)まで移動する機能と言える。
以上から次のからくりがわかる。
- [からくり1]nが偶数になる毎に発生する”右に1ビットシフト”により、数値の基準点となる最下位ビット(20の桁)がSTEP:0(開始時)のn の最下位ビットから左にずれる
- [からくり2]数値の基準点が左にずれるため、”+1″する位置も同様にずれる
また、この例では、10進数で見た時はn=”1″に到達したSTEP:26(切り捨て分の”0“を含めたとき218)をSTEP数としているが、2進数で見た時はSTEP:22の時点で218に到達しており、STEP数に違いがある。
- [からくり3]10進数で見た時はn=”1″に到達した時点を”STEP数”としているが、2進数で見た時は2のべき乗となったときを到達点と判断でき”STEP数”に違いがある
[からくり1]と[からくり2]から数値の基準点がずれるのがコラッツ予想を直感的に理解するのを難しくしている理由である 。
対象を観測したいのに、その基準点がずれているのだから、理解が難しいのは当然である。
[からくり3]に対して、理解が難しい要因になっているかの判断はできない。
ただし、STEP数を求めることは命題ではないので追及はしない(ただし次回で利用する)。
今回のまとめ
からくり
- [からくり1]nが偶数になる毎に発生する”右に1ビットシフト”により、数値の基準点となる最下位ビット(20の桁)がSTEP:0(開始時)のn の最下位ビットから左にずれる
- [からくり2]数値の基準点が左にずれるため、”+1″する位置も同様にずれる
- [からくり3]10進数で見た時はn=”1″に到達した時点を”STEP数”としているが、2進数で見た時は2のべき乗となったときを到達点と判断でき”STEP数”に違いがある
[からくり1]と[からくり2]が、コラッツ予想を直感的に理解することを難しくしている理由である。
[からくり3]は命題ではないので追及はしない
次回「結論&証明」編
次回は、コラッツ予想を直感的に理解することを難しくしている”からくり”を回避し、また[論理E]の証明を含めて、結論を導きだし、コラッツ予想の真偽を確認する。
関連情報
コラッツ予想の式
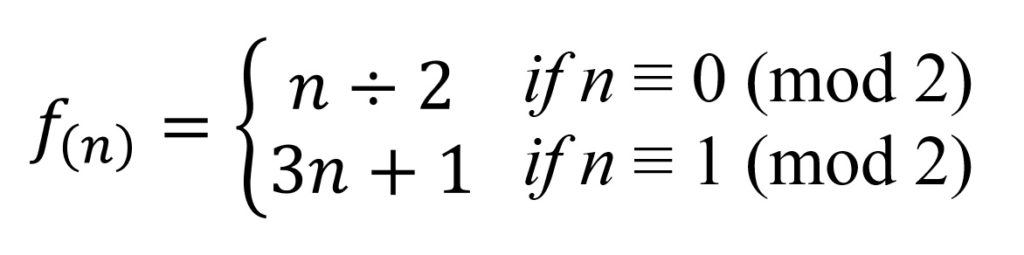
“2”より”3″が大きいのに、すべての正の整数のどの値で開始しても、nは増加傾向にならず、減少して”1″に到達する(その後”1→4→2→1→…”の無限ループになる)という予想。
このように矛盾した結果にたどり着くのは、何故なのか?
関連投稿
徹底解説 コラッツ予想のからくり
これらの投稿は下記の「コラッツ予想をプログラマーが検証してみた」の要点のみ抽出し再構築、説明不足だった部分を加筆してまとめたものです。
#1 特徴&論理編
#2 からくり編(本投稿)
#3 結論&証明編(2021/11/15追記)
コラッツ予想のからくりのまとめ (2021/12/20追記)





コメント
I like your content very much. You visit again. Thanks for the article
Thank you for your comment. It’s encouraging.