説明不足覚悟で”とても簡単”に言うと次となる。
n/2が2進数では右に1ビットシフトとなる。
3n+1を無限に繰り返すと2のべき乗に収束する。
この2つの組み合わせで結果的にn=1に到達する。
本記事に関連する新しい投稿があります(2023/07/05,2023/11/03追記)
簡単に言うと
日本語版

上記は画像なので同じ文を記述して置く。
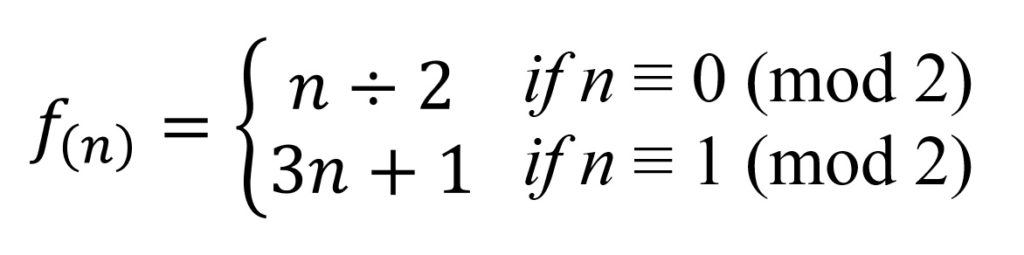
コラッツ予想とは、
上記の式に対して
すべての正の整数のどれかのnで開始し
結果を次のf(n)の入力として繰り返しても、
最終的に1に到達する
(正確には1→4→2→1→…と無限ループになる)
と言う予想です。
“2”より”3″が大きいのに、
増加し続けずに減少して”1″に到達してしまう。
このように矛盾した結果にたどり着くのは、何故なのか?
簡単に言うと
偶数(2で割った余り:modが0)時のn÷2(n/2)が
2進数では”右に1ビットシフト“であり、
最下位ビットの”0″を切り捨てて行くが、
数値の要素である“1”を含むビットパターンは変わらない。
奇数(2で割った余り:modが1)時の3n+1の”3n”は
nのすべての桁を等しく3倍するが、
“+1″は下位の桁にのみ作用し、
上位の桁より下位の桁が速く増加する。
nは奇数なので3倍しても奇数となり
それに”+1″すると必ず偶数となるため、
nの下位の桁に2のべき乗を含む(2の0乗=1は奇数なので除外)。
このため、3n+1を無限に繰り返すと
2のべき乗に収束する。
2のべき乗は、2進数で見ると
“1”が立っているビットが1つのみで、
下位の桁には”0″が続く。
この2つの組み合わせで結果的にn=1に到達する。
n/2でビットパターンが変わらないことにより、
3n+1の無限に繰り返しが成り立ちます。
その後も1→4→2→1→…と無限に2のべき乗を繰り返すため、
無限に存在するすべての正の整数がn=1に到達することを
表しています。
詳細は、下記の「関連投稿」を参照ください。
英語版(2022-02-26追記)
The Collatz Karakuri(Mechanism)
If n/2 is a binary number, it shifts 1 bit to the right.
Repeating 3n+1 infinitely converges to a power of 2.
As a result, n=1 is reached by these combinations.
#CollatzKarakuri #CollatzProblem #CollatzConjecture #Collatz #コラッツ予想のからくり

The Japanese version is the original.
It’s a slightly modified machine translation, so there may be some weird parts.
In that case, please advise “this kind of expression is better”.
Put simply.
n÷2 (n / 2) when even (remainder divided by 2: mod is 0) In binary, it is ” 1 bit shift to the right “, The least significant bit ” 0 ” is truncated, The bit pattern containing the numerical element ” 1 ” does not change.
“3n” of when odd (remainder divided by 2: mod is 1) triples all digits of n equally, but “+1” acts only on the lower digits, increasing the lower digits faster than the upper digits
Since n is an odd number, it will be an odd number even if it is multiplied by 3, and if it is “+1”, it will always be an even number.
Even numbers include a power of 2 in the lower digits (excluded because 2 to the 0th power = 1 is an odd number).
Therefore, if 3n + 1 is repeated infinitely, it converges to a power of 2.
The power of 2 has only one bit in which “1” stands when viewed in binary.
The lower digits are followed by “0”.
As a result, n = 1 is reached by these combinations.
By not changing the bit pattern at n / 2,
Infinite repetition of 3n + 1 holds.
After that, it repeats 1 → 4 → 2 → 1 → … infinitely to a power of 2, which means that all infinitely existing positive integers reach n = 1.
特徴&論理&からくり&結論のまとめ
特徴
コラッツ予想の式から以下の特徴が抽出できる。
- [特徴1]偶数と奇数の2種類の数値を扱うこと
- [特徴2]n/2が2進数では”右に1ビットシフト”であること
- [特徴3]到達点の”1″、および、”1→4→2→1→…”の無限ループの各数値が、2のべき乗(1=20, 2=21, 4=22)であること
これらの特徴からコラッツ予想の式は”2進数”との親和性が高いことが分かる。
詳細は、徹底解説 コラッツ予想のからくり#1 特徴&論理編 を参照してください。(2022/05/13追記)
論理
コラッツ予想の式から以下の論理が導き出せる
- [論理A]nを2進数で見たとき、最下位ビット(20の桁)が”0″であれば偶数、”1″であれば奇数である
- [論理B]”n/2″は2進数では”右に1ビットシフト”であり、数値の要素となる”1″を含んだビットパターンは変わらない
- [論理C]”3n+1″の結果は必ず偶数となり、下位の桁のグループに2のべき乗を含む
- [論理D]”3n+1″の”+1″により、上位の桁のグループより下位の桁のグループの方が速く増加する
- [論理E]”3n+1″を無限に繰り返すと、nそのものが2のべき乗(“1″が立っているビットが1つ)に収束する
(2022/02/23追記:「論理E:要証明」となっていましたが#3 結論&証明編にて証明済みのため「要証明」部分を削除しました)
詳細は、徹底解説 コラッツ予想のからくり#1 特徴&論理編 を参照してください。(2022/05/13追記)
からくり
コラッツ数列に、[論理A~E]を当てはめ、次のからくりが得られた。
- [からくり1]nが偶数になる毎に発生する”右に1ビットシフト”により、数値の基準点となる最下位ビット(20の桁)がSTEP:0(開始時)のn の最下位ビットから左にずれる
- [からくり2]数値の基準点が左にずれるため、”+1″する位置も同様にずれる
- [からくり3]10進数で見た時はn=”1″に到達した時点を”STEP数”としているが、2進数で見た時は2のべき乗となったときを到達点と判断でき”STEP数”に違いがある
- [からくり4]”+1″の数値の基準点が開始時のときより左にずれているため、比較的少ないSTEP数で”1″に到達する。
詳細は、徹底解説 コラッツ予想のからくり#2 からくり編 を参照してください。(2022/05/13追記)
結論
[からくり1]と[からくり2]の対策により以下の結論を得た。
- [結論1] [論理B]により「n/2が”右に1ビットシフト”である」こと、および「数値の要素となる”1″を含んだビットパターンは変わらない」こと、[論理E]の「nそのものが2のべき乗に収束する」ことから、無限に存在するすべての正の整数は”1″に到達する。
- [結論2] “1→4→2→1→…”の無限ループは、偶数時の”n/2″により同じ値に見えるだけで、その実体は無限ループしているわけではなく、また他の値で無限ループすることも無い。
詳細は、徹底解説 コラッツ予想のからくり#3 結論&証明編 を参照してください。(2022/05/13追記)
連絡先
一連の投稿に対して、賛否のご意見、投稿内容の間違い、ご要望などありましたら、ハッシュタグ「#コラッツ予想のからくり #プログラミングの深淵を求めて」を付けてツイートしてください。
または、Twitter @dratech2020 の投稿に返信ください。
関連投稿
コラッツ予想の第一印象(2023/10/24追記)
iCollatzの提案(2023/06/23追記)
ツール:Excel版(2021/12/25追記)
(2023/1/19追記)
利用方法については、”コラッツ予想をプログラマーが検証してみた”の #2 Excelで作ってみた および #3 さらに角度を変えて検証したら・・・!!! を参照ください。
ツール:ブラウザ(BigInt)版(2021/12/25追記)
(2023/1/19追記)
スパコンで10進数の21桁ぐらいまで隙間(奇数開始と予想)なく確認しているのに対して、ピンポイントでの数値指定の開始となりますが10進数100桁や1000桁など非常に大きい数値での検証が可能です。
ツールはJavascript(画面描画にjQueryを利用)で作ってあり、日常ご利用のWebブラウザのみで動作します(演算時はサーバー通信もありません)。
Web開発経験のある方はご存じと思いますがソースコードを参照することができオープンで透明性があるものです。
関連記事: JavascriptのBigIntの限界値を探る
徹底解説 コラッツ予想のからくり
これらの投稿は下記の「コラッツ予想をプログラマーが検証してみた」の要点のみ抽出し再構築、説明不足だった部分を加筆してまとめたものです。
コラッツ予想をプログラマーが検証してみた
#1 要件を確認する
#2 Excelで作ってみた
#3 さらに角度を変えて検証したら・・・!!!
#4 最後に
コラッツ予想のからくり Extra Stage
#1 「1→4→2→1→…のループ」がすべてを飲み込む!? (2022-05-13追記)
#2 コラッツ数列は偶数奇数以外に仕分けできる!? (2022-06-25追記)
プログラミングテクニック(2023/03/15追記)
プログラミングテクニック アルゴリズム+データ構造=プログラム
プログラミングテクニック 究極のプログラミングでプロダクトライフコストを削減する





コメント